Hydraulic Design

Hydraulic Design

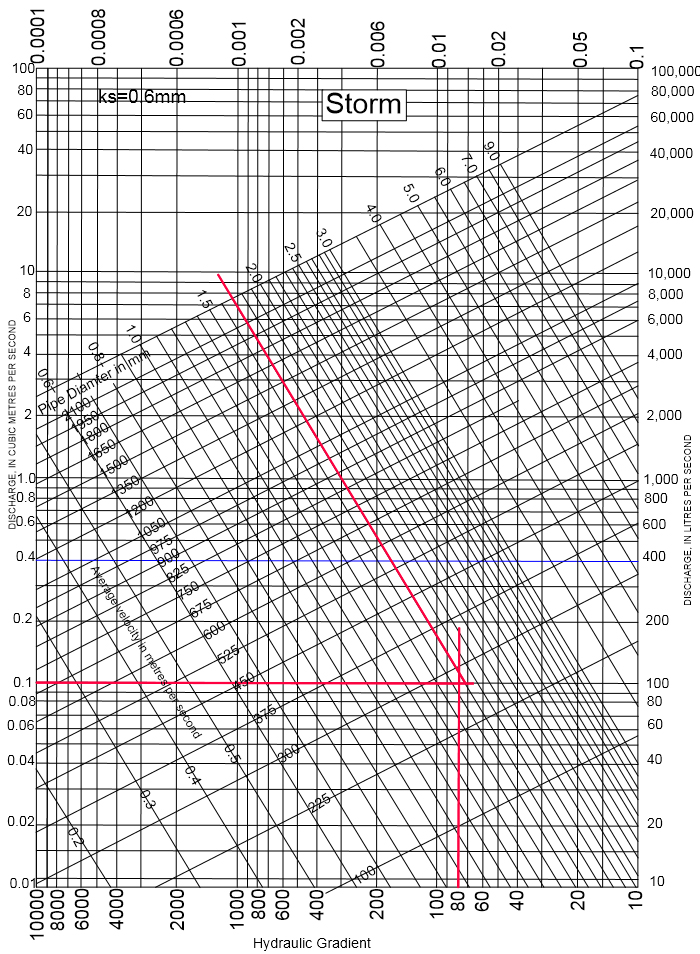
The Colebrook – White equation provides the most accurate results to assist in gravity sewer design. Hydraulic flow charts published in “Tables for hydraulic design of pipes, sewers and channels” 7th edition are most commonly used to simplify the Colebrook – White equation. Once a pipe roughness coefficient (ks) is determined, the corresponding flow chart details four variables, i.e. pipe internal diameter, water velocity, hydraulic gradient and discharge. Once two of the variables are known, the remaining two variables can be determined.
CCW twinwall pipes have a smooth inner wall giving excellent hydraulic performance. Sewers for adaption 6th edition stipulates a minimum roughness coefficient (ks) of 0.6mm for surface water sewer design and a minimum velocity of 1.0m/sec pipe full flow.

COLEBROOK – WHITE EQUATION

A number of formulas have been developed to assist in hydraulic calculations to determine flow rates in pipelines. The Colebrook – White equation is considered most accurate for commercial pipes as effective roughness is applied.

The equation expressed in Engineering terms is as follow:

Relative Velocity and Flow in Circular Pipe for any Depth of Flow

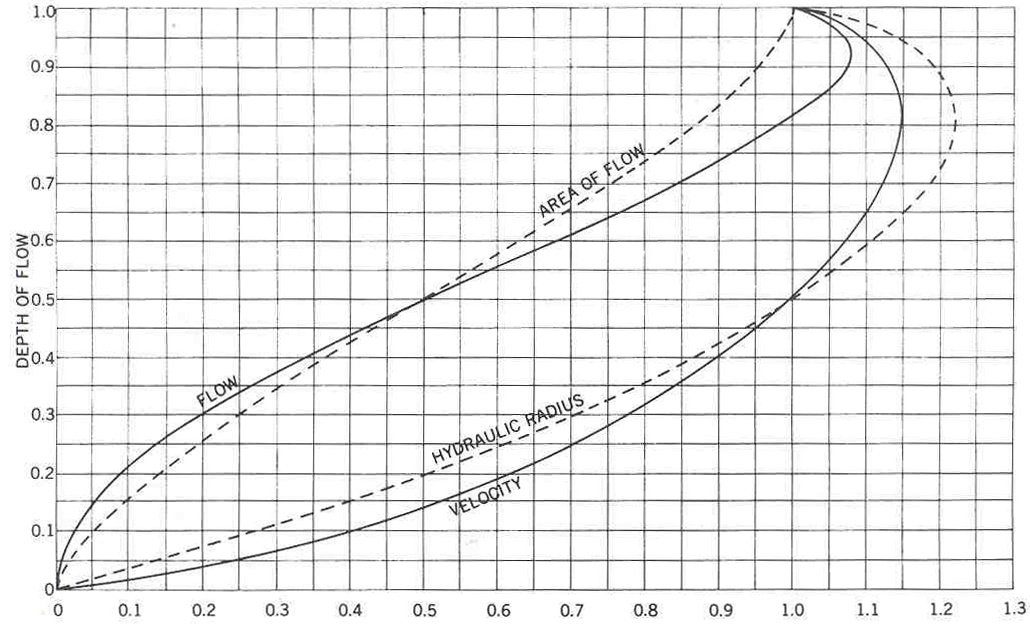
NOTE: This graph complies with B.S. 8005: part 1 1987 and will comply to any new Irish, British or European Standards in the future.

Design Example

Design of storm water sewer where ks = 0.6mm and minimum velocity = 1.0m/sec.
Length of pipe = 1200m
Fall to outlet = 15m => gradient of 1:80
Design Discharge 0.1m³/sec

Determine pipe size when flowing full.
Pipe size required is >225mm Ø, next available size is 300mm Ø
Check velocity for 300mm Ø pipe @ gradient of 1:80 = 1.7m/sec
1.7m/sec > 1.0m/sec, therefor satisfactory

What is the pipe size required when the pipeline is flowing 35% full for the same discharge?
Using the chart “Relative Velocity and Flow in a Circular Pipe for any Depth of Flow” proportional
discharge is 0.27 m³/sec when flowing at 35% full.
Discharge 0.1m³/sec ÷ 0.27 m³/sec = 0.37 m³/sec.
Return to ks 0.6 flowchart and extend a horizontal line at 0.37 m³/sec discharge to meet vertical line
of 1:80 gradient.
Pipe size required is 450mm Ø CCW TW pipe.
Check velocity 2.3m/sec x proportional velocity of 0.85 = 2.0m/sec
Therefore satisfactory.